Material I: innermathematische Einstiege
Computergrafik
 Lösungen/Kontrolle

Lösungshinweise zu Computergrafik mit linearen Funktionen

a.
Punkt P und beliebig gewählte Steigungen ergeben verschiedene Geraden mit dieser geforderten Bedingung oder Punkt P und ein beliebig gewählter zweiter Punkt ergeben auch verschiedene Geraden, die die angegebene Bedingung erfüllen.

allgemeine Form (Geradenschar):

Gegegeben P (-3|4) und beliebige Steigung t (beliebig gewählter Parameter-Name). Man erhält:
y = t*x +(3t + 4). Man kann auch den jeweils unterschiedlichen y-Achsenabschnitt mit k z.B. bezeichnen und erhält dann eine Funktionsgleichung mit dem Parameter k.verwendete

Zusammenhänge: Zweipunkte-Gleichung, Punkt-Steigung-Form, Geradenbüschel


b.
Wahl eines passenden Koordinatensystems, z.B.der y-Achse durch die beiden Schnittpunkte der Geradenbüschel, x-Achse durch den unteren Schnittpunkt ergibt besonders einfache Gleichungen/Geradenbüschel.

a) y = m*x+ 4 wobei m von -2 bis 2 in Abständen von 0.5 durchläuft

b) y= k*x wobei k von -2 bis 2 in Abständen von 0.5 durchläuft.
verwendete Zusammenhänge: Steigung, y-Achsenabschnitt, Geradenbüschel

 

c. bei Derive Arbeiten mit der Infos in der Toolbox CHI-Funktion.
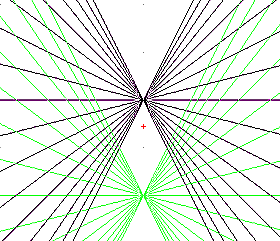
blauer Strahlrechts:
y = x im Intervall [0,2]
y = 0,5x + b und Punkt P (2|2) für die Gerade im Intervall [2,4]
y = 0,25 x + c und Punkt Q (4|3) für die Gerade im Intervall [2,6]

gelber Strahl rechts: Beachte, wie sich die Steigungen in den verschiedenen Bereichen eines Strahl nacheinander verändern (siehe blauer und roter Strahl); die Koordinaten der Punkte, an denen der neue Bereich mit Knick beginnt, kannst Du ablesen.

grüner Strahl rechts: m=2 im Intervall [0,2]

linke Äste: Was mußt du bei den bisherigen Ergebnissen jeweils ändern?

Beispiel "rote Strahlen"

im Intervall [-2, 0] y= - 2x y= 2 x im Intervall [0,2]
im Intervall [-4,-2] y= - x- 2 y= x + 2 im Intervall [2,4]
im Intervall [-6,-4] y= -0.5x - 4 y= 0.5x + 4 im Intervall [4,6]

verwendete Zusammenhänge: Zweipunkte-Gleichung, Punkt-Steigung-Form, Koordinaten von Punkten auf einer Gerade bestimmen (abschnittsweise definierte Funktion)

 

zurück
Hauptmenü